TILJavaScriptLinkedList Tree

JavaScript ES6 LinkedList, Tree

, ,

Javascript LinkedList

  • Linked List
  • Tree

Linked List

Linked List

Array vs Linked List

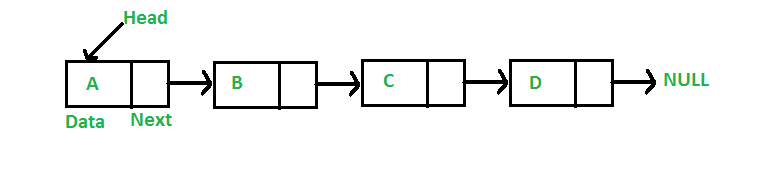
Array vs Linked List

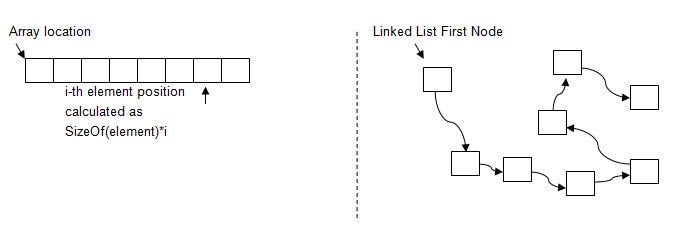
Array vs Linked List

  • Size => Fixed vs Dynamic
  • Insert => Hard vs Easy
  • Deletion => Hard vs Easy
  • Random Access(원하는 곳에 한번에 접근할 수 있다) => Allowed vs Not allowed
  • Extra memory space => doesn’t need vs required
Array vs Linked List
o(1) access o(n)
o(n) search o(n)
o(n) insert o(1)
o(n) remove o(1)

Create Linked List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
function LinkedList(){
	//define Node
	var Node = function(element){
		this.element = element;
		this.next = null;
	};

	var length = 0;
	var head = null;


	//값을 추가하는 method
	this.append = function(element){
		var node = new Node(element), current;
		
		if(head === null){
			head = node;
		}else {
			current = head;
			// current값이 null일때 까지 돌아간다.			
			while(current.next){
				current = current.next;
			}
			// 마지막값에 node를 집어넣는다.
			current.next = node;
		}
		length++;
	};

	//특정 위치의 값을 제거하는 method
	this.removeAt = function(position){
		if(position > -1 && position < length){
			var current = head, previous, index=0;

			if(position === 0){
				head = current.next;
			}else {
				while(index++ < position){
					previous = current;
					current = current.next;
				}
				// 이전값을 덮어 씌운다.
				previous.next = current.next;
			}
			// 값이 1개 지워졌음으로 1 감소.
			length--;
		
			return current.element;
		}else {
			return null;
		}
	};

	// 값을 추가한다.
	this.insert = function(position, element){
		if(position >= 0 && position <= length>){
			var node = new Node(element), current = head, previous, index = 0;
			
			//head 에다가 insert를 해주려고 할떄
			if(position === 0){
				node.next = current;
				head = node;
			} else {
				while(index++ < position){
					previous = current;
					current = current.next;
				}

				node.next = current;
				privious.next = node;
			}
			length++;

			return true;
		}else {
			return false;
		}
	};
	
	// remove 요소를 제거한다.
	this.remove = function(element){
		var index = this.indexOf(element);
		return this.removeAt(index);
	};

	this.indexOf = function(element){
		var current = head, index = 0;

		while(current){
			if(element === current.element ){
				return index;
			}
			index++;
			current = current.next;
		}
		return false;
	};

	this.isEmpty = function(){
		return length === 0;
	};

	this.size = function(){
		return length;
	};

	this.toString = function(){
		var current = head, string = '';

		while(current) {
			string += current.element;
			current = current.next;
		}
		return string;
	};

	this.getHead = function(){
		return head;
	};


}

Tree

Tree

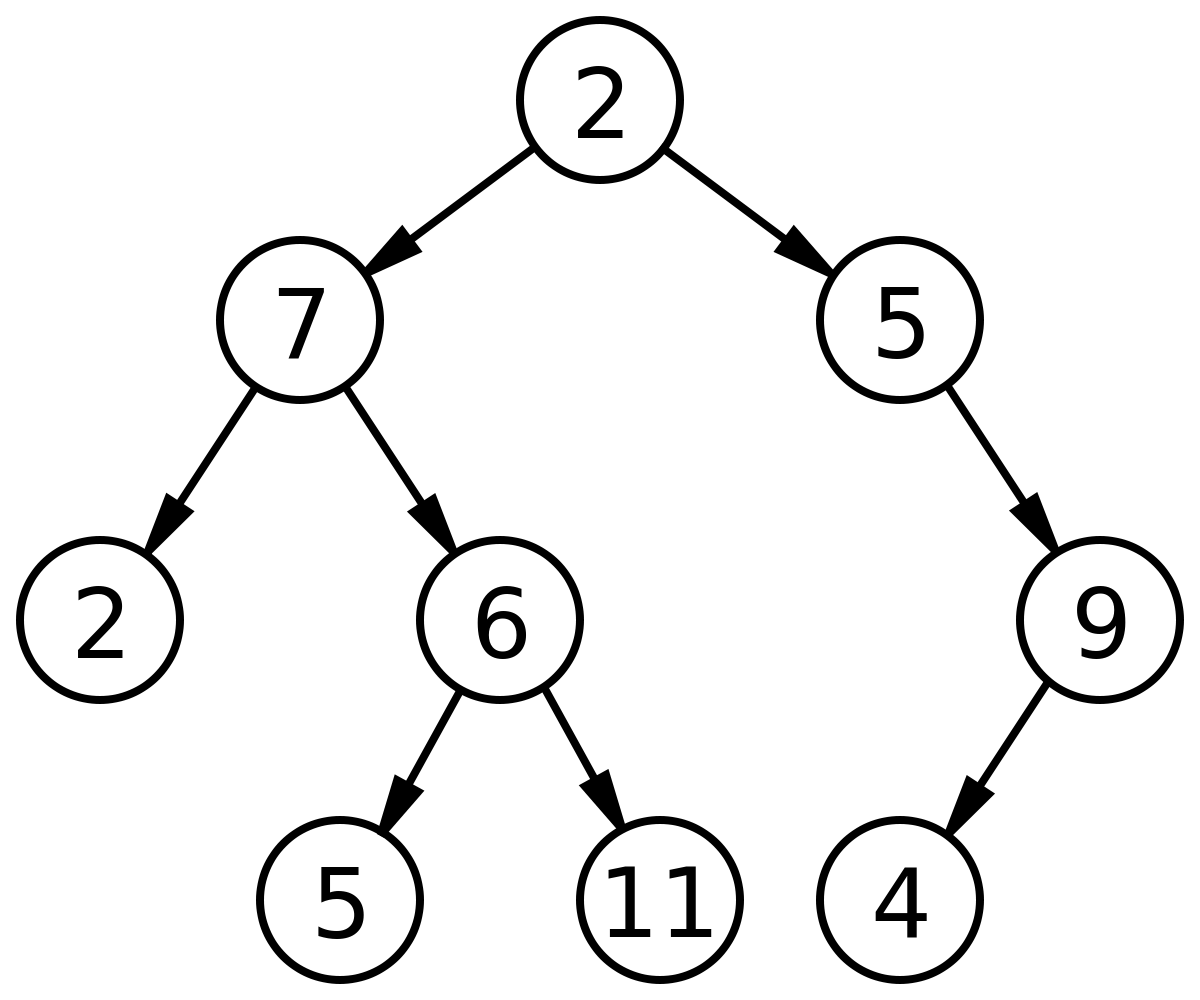
  • root: 2
  • level: (0 ~ 3)
  • child of 2: 7,5
  • subtree: 6,5,11
  • Node: (9)
  • edge: (8)

Binary Search Tree

2진 탐색 트리이다. 왼쪽에는 작은값 오른쪽에는 큰 값이 존재한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

function BinarySearchTree(){
	var Node = function(key){
		this.key = key;
		this.left = null;
		this.right = null;
	};

	var root = null;


	function insertNode(node, newNode){

		if(newNode.key < node.key){
			if(node.left === null){
				node.left = newNode;
			}else {
				insertNode(node.left, newNode);
			}
		}else {
			if(node.right === null){
				node.right = newNode;
			}else {
				insertNode(node.right, newNode);
			}
		}
	};

	this.insert = function(key){
		var newNode = new Node(key)

		if(root === null){
			root = newNode;
		}else {
			insertNode(root, newNode);
		}
	};

}

Binary Search Tree - inOrderTraverse

  • 왼쪽 가운데 오른쪽 순서로 탐색한다.
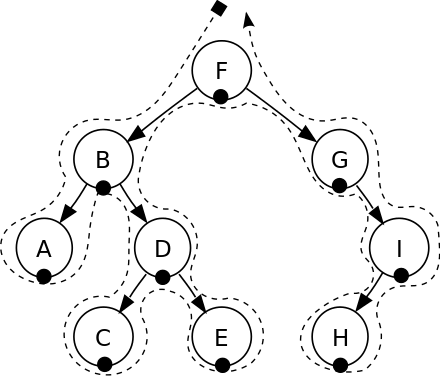
    inOrderTraverse 
1
2
3
4
5
6
7
8
9
10
11
var inOrderTraverseNode = function(node, callback){
	if(node !== null){
		inOrderTraverseNode(node.left, callback);
		callback(node.key);			
		inOrderTraverseNode(node.right, callback);
	}
}

this.inOrderTraverse = function(callback){
	inOrderTraverseNode(root, callback);
};

Binary Search Tree - preOrderTraverse

  • 가운데 왼쪽 오른쪽 순서로 탐색한다.
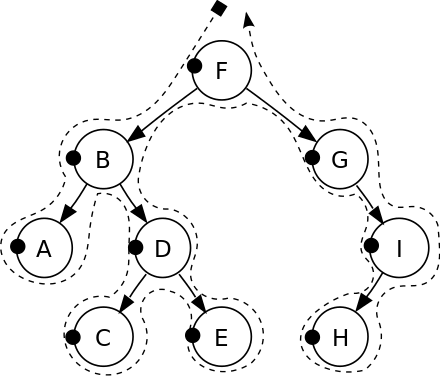
    preOrderTraverse 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
// preOrderTraverse

function BinarySearchTree(){
	var Node = function(key){
		this.key = key;
		this.left = null;
		this.right = null;
	};

	var root = null;


	function insertNode(node, newNode){

		if(newNode.key < node.key){
			if(node.left === null){
				node.left = newNode;
			}else {
				insertNode(node.left, newNode);
			}
		}else {
			if(node.right === null){
				node.right = newNode;
			}else {
				insertNode(node.right, newNode);
			}
		}
	};

	this.insert = function(key){
		var newNode = new Node(key)

		if(root === null){
			root = newNode;
		}else {
			insertNode(root, newNode);
		}
	};

	// preorderTraverse

	var preOrderTraverseNode = function(node, callback){
		if(node !== null){
			callback(node.key);
			preOrderTraverseNode(node.left, callback);
			preOrderTraverseNode(node.right, callback);
		}
	}

	this.preOrderTraverse = function(callback){
		preOrderTraverseNode(root, callback);
	};

	function printNode(value) {
		console.log(value);
	}
}

Binary Search Tree - postOrderTraverse

  • 오른쪽 가운데 왼쪽 순서대로 탐색한다.
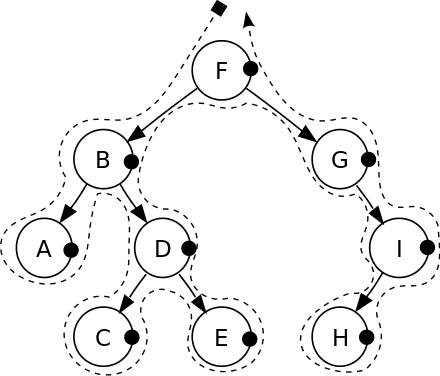
    postOrderTraverse
1
2
3
4
5
6
7
8
9
10
11
var postOrderTraverseNode = function(node, callback){
	if(node !== null){
		postOrderTraverseNode(node.right, callback);
		callback(node.key);						
		postOrderTraverseNode(node.left, callback);
	}
}

this.postOrderTraverse = function(callback){
	postOrderTraverseNode(root, callback);
};

Binary Search Tree - find min/max value

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

this.min = function(){
	return minNode(root);
};

var minNode = function(node){
	if(node){
		while(node && node.left !== null){
			node = node.left;
		}

		return node.key;
	}
	
	return null;
};


this.max = function(){
	return maxNode(root);
};

var maxNode = function(node){
	if(node){
		while(node && node.right !== null){
			node = node.right;
		}

		return node.key;
	}
	
	return null;
};

Binary Search Tree - find specific value

  • 특정 값을 찾기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

	this.search = function(){		
		return searchNode(root, key);
	};

	var serachNode = function(node, key){
		if(node === null){
			return false;
		}
		if(key < node.key){
			return searchNode(node.left, key);
		} else if(key > node.key){
			return searchNode(node.right, key);
		} else {
			return true;
		}
	}

console.log(tree.search(1) ? 'Key 1 found.' : 'Key 1 not found.');

gulp

1
2
$ npm install --save-dev gulp-imagemin

gulp-imagemin : image minify

1
2
3
4
5
6
7
gulp.task("imagemin", function(){
	pump([
		gulp.src(publicPath.src + 'img/*.jpg'),
		imagemin(),
		gulp.dest(publicPath.dest + 'img/')
	]);
});

css minify(gulp-clean-css) : css minify

1
2
3
4
5
6
7
gulp.task("cleancss", function(){
	pump([
		gulp.src(publicPath.src + 'css/minify.css'),
		cleancss(),
		gulp.dest(publicPath.dest + 'css/')
	]);
});

gulp-sass : convert .scss to .css

1
2
3
4
5
6
7
gulp.task("sass", function(){
	pump([
		gulp.src(publicPath.src + 'sass/*.scss'),
		sass().on('error', sass.logError),
		gulp.dest(publicPath.dest + 'css/')
	]);
});

gulp-concat-css : concatenate css files

1
2
3
4
5
6
7
gulp.task("concatcss", function(){
	pump([
		gulp.src([publicPath.src + 'css/concat1.css', publicPath.src + 'css/concat2.css']),
		concat('concatenated.css'),
		gulp.dest(publicPath.dest + 'css/')
	]);
});

clean(del)

1
2
3
gulp.task("clean", function(){
	return del.sync([publicPath.dest + 'js/*.js', publicPath.dest + 'css/*.css', publicPath.dest + 'img/']); 
});

watch

1
2
3
4
5
gulp.task("watch", function(){
	gulp.watch("public/src/*.js", ["uglify"]);
});

gulp.task("default", ["uglify", "watch"]);

watch

1
2
3
4
5
6
gulp.task("watch", function(){
	gulp.watch(publicPath.src + 'js/*.js', ["uglify", "concat"]),
	gulp.watch(publicPath.src + 'css/*.css', ["cleancss", "concatcss"]),
	gulp.watch(publicPath.src + 'img/*.jpg', ["imagemin"]),
	gulp.watch(publicPath.src + 'sass/*.scss', ["sass"])
 +});
Share